Математические модели трехмерного моделирования обледенения для аэродинамических поверхностей
Номер РФФИ проекта: 19-29-13016 мк
Руководитель проекта: Стрижак Сергей Владимирович
Аннотация проекта
Актуальность задач по обеспечению безопасности и надежности полетов, а также защиты летательных аппаратов (ЛА) от катастроф, в том числе в северных районах Российской Федерации, все более возрастает в связи с появлением новых типов конструкций, перспективных технологий и материалов, в том числе, полимерных композиционных, из которых изготавливают основные силовые элементы и агрегаты таких технических объектов. Одной из актуальных задач в авиации является проблема изучения и моделирования процесса ледообразования. Необходимость борьбы с обледенением затрагивает не только классические объекты, такие как воздушные и морские суда, но и беспилотные ЛА, провода электропередач, взлетно-посадочные полосы. В частности, задачи обледенения крайне актуальны в условиях Арктической зоны Российской Федерации для региональной авиации. Нарастание льда, ледяного налета, снега на крыле и хвостовом оперении лёгкого конвертируемого самолёта, перспективного самолета местных воздушных линий, при определённых условиях, происходит очень быстро и неравномерно, что приводит к уменьшению подъемной силы крыла до 30% и увеличению лобового сопротивления на 40%.
Междисциплинарность работы состоит в рассмотрении явления ледообразования с использованием основных законов механики жидкости и газа, физических моделей для налипания кристаллов льда и динамики жидкой пленки, модели для полидисперсной смеси капель, лабораторного эксперимента в различных дозвуковых аэродинамических установках на моделях, изготовленных при помощи аддитивных SLA технологий, численного моделирования, аддитивной технологии для изготовления экспериментальных моделей. Значимость работы состоит в том, что разрабатываемый программный комплекс для моделирования процессов ледообразования будет открытым ПО и может быть использован на авиационных предприятиях, в конструкторских бюро, в научных организациях РФ.
Научная новизна работы состоит в уточнении модели для барьерного льда с учетом динамики жидкой пленки, движущейся на поверхности твердого тела, новой модели для полидисперсной смеси капель в разработке нового расчетного кода. Результатом работы будет программный комплекс для моделирования процессов ледообразования (рогообразный, барьерный, желобообразный), расчеты, экспериментальные модели крыла c различными законами нарастания льда, изготовленными при помощи аддитивной SLA-технологии на базе промышленных 3D принтеров, с механическими свойствами близкими к свойствам ПКМ, и проведение верификации и контроля соответствия характеристик элементов ЛА современным нормам летной годности.
Результаты 2020 года работы
Участниками проекта разработан прототип решателя iceFoam на базе свободного пакета OpenFOAM v1912 для моделирования динамики жидких частиц и образования льда на поверхности исследуемого тела. Пока решатель предназначен для частиц с характерным размером порядка 40 мкм, что соответствует Приложению C Авиационных правил АП-25. Ведутся работы по расширению возможностей решателя (в направлении моделирования различных режимов и типов нарастания льда) на базе открытых пакетов Yade и OpenFOAM для Приложения «Снег и метель».
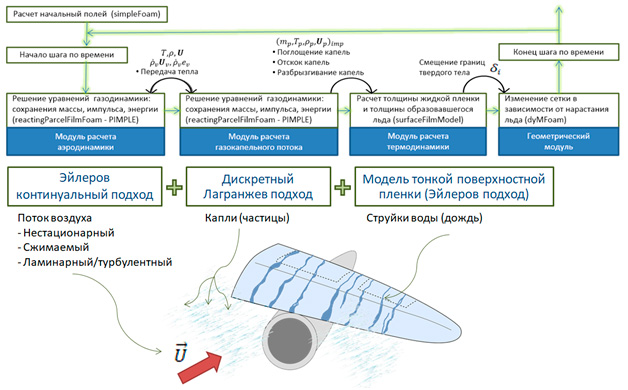
Моделирование многофазных потоков с континуальной и дисперсной фазами проводится с использованием Эйлер-Лагранжев подхода, в котором непрерывная фаза рассматривается в Эйлеровой постановке, в то время как капли-частицы в дисперсной фазе отслеживаются в Лагранжевой постановке. В настоящий момент iceFoam включает в себя базовый решатель и две библиотеки: одна библиотека реализует термодинамическую модель жидкой пленки по теории мелкой воды libsurfaceFilmModelsSWIM, вторая библиотека предназначена для расчета капель-частиц libIceFoamParticles. В расчете используется две сетки: одна для моделирования внешнего газокапельного потока, другая, толщиной в одну ячейку, для расчета нарастания льда. Нарастание льда приводит к изменению начальной формы тела. Граница тела перемещается в пространстве по нормали. При этом при пересчете положения узлов сетки необходимо обеспечить одновременное перемещение границ для двух разных сеток. Одним из эффективных способов такого пересчета является использование решения уравнения Лапласа. Общая структура решателя iceFoam показана на рисунке 1.
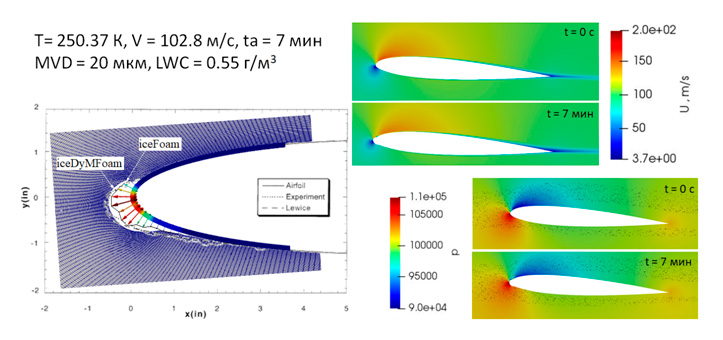
Решены тестовые задачи расчета замерзания льда на цилиндре, профиле NACA0012 и GLC-305 с помощью метода URANS и высокорейнольдсовой модели турбулентности Spalart-Allmares (Рис. 2).

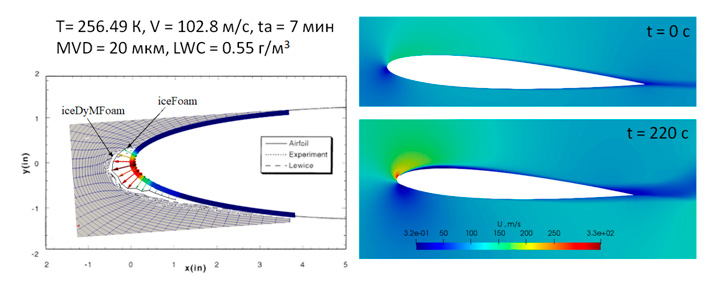
Математическая модель для моделирования снежинок
В работе используется Эйлер-Лагранжев подход — сопряженный метод на базе методов вычислительной гидродинамики и метода дискретных элементов (МДЭ).
В стандартном Эйлерово-Лагранжевом моделировании нагруженных частицами многофазных потоков частицы рассматриваются как точечные массы. Поток на уровне частиц не разрешен, и для описания взаимодействия жидкости и частиц используются аналитические/эмпирические модели гидродинамических сил.
Метод дискретных элементов
Метод дискретных элементов (МДЭ) или Discrete Element Method (DEM) — это Лагранжев метод, в том смысле, что все частицы в вычислительной области отслеживаются путем явного решения их траекторий. МДЭ хорошо подходит для изучения поведения большого количества частиц на микроскопическом уровне, например для описания движения, осаждения, агломерации или агрегации большого количества адгезивных частиц, в том числе погруженных в потоки жидкости или газа.
В зависимости от программного обеспечения данный метод даёт возможность отслеживать упругие взаимодействия частиц, их деформации, взаимодействие с учётом трения, сил когезии и адгезии, исследовать влияние температуры и давления, а также механического воздействия при моделировании сложных систем. В том числе систем сложной геометрии, подвижных или вращающихся систем.
При объединении с гидродинамическим решателем исследовать динамику частиц можно в развитом потоке жидкости или газа, с учётом взаимодействия среды с частицами.
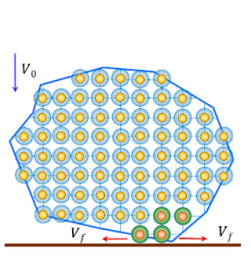
Основные принципы метода дискретных элементов (МДЭ), он же DEM, заключаются в следующем. Моделирование начинается c помещения всех частиц в конкретное положение и придания им начальной скорости. Затем силы, воздействующие на каждую частицу, рассчитываются, исходя из начальных данных и соответствующих физических законов.
Уравнения в МДЭ решаются с помощью явных схем по времени. В связи с этим все силы, действующие на частицу, складываются, чтобы определить результирующую силу. Изменение в положении и скорости каждой частицы в течение определенного временного шага рассчитывается из законов Ньютона методом интегрирования. После этого новое положение используется для расчёта сил на следующем временном шаге, и этот цикл программы повторяется до тех пор, пока моделирование не закончится.
Метод вычислительной гидродинамики
Для описания аэродинамики потока используется классический гидродинамический подход с использованием метода конечных объёмов для решения уравнений Навье-Стокса. Данный подход является Эйлеровым. Поток в исследуемых задачах предполагается несжимаемым.
Программное обеспечение
Для расчёта поставленной задачи используется объединение двух свободно распространяемых пакетов с открытым исходным кодом: YADE и OpenFOAM.
- Расчёт частиц сложной формы;
- Расчёт сложных моделей взаимодействия частиц (с учётом когезии, трения, упругости, деформации, анизотропии и других свойств материала);
- Работа решателя в параллельном режиме с использованием MPI библиотеки.
- Хорошая документированность;
- Модульное устройство кода на базе C++;
- Широкое распространение;
- Многочисленность разработчиков и пользователей;
- Большой опыт имплементации новых моделей.
Разработка решателя snowFoamYade
Решатель snowFoamYade основан на базе решателя icoFoamYade, в котором частички представлены как точечные массы, на которые действует гидродинамическая сила сопротивления. В решателе icoFoamYade данная сила, представлена силой лобового сопротивления Стокса, которая не подходит для расчёта динамики снежных кристаллов. Японским учёным Ишизако была рассчитана сила сопротивления для снежного кристалла, являющаяся функцией числа Рейнольдса по диаметру частицы в степени -0.28. В решателе snowFoamYade сила сопротивления рассчитывается по формуле Ишизаки.
Алгоритм решения
- Обмен информацией с CFD расчётом (определение гидродинамических сил, действующих на частицы);
- Обновление сил, приложенных к частицам по результатам предыдущего шага;
- Приблизительное обнаружение столкновений («pass 1»);
- Обнаружение точных столкновений тел, обновление взаимодействий по мере необходимости;
- Расчёт взаимодействий при приложении сил к телам;
- Приложение других внешних сил (например, гравитации и гидродинамических сил);
- Изменение положения тел на основе сил, путем интегрирования уравнений движения;
- Обмен информацией (ускорение, скорость, масса и координаты частиц) с CFD расчётом.
- Получение информации от DEM решения (ускорение, скорость, масса и координаты частиц);
- Корректируются поля давления, скорости, плотности;
- Решается закон сохранения количества движения;
- Решение уравнения неразрывности для коррекция поля давления;
- Коррекция поля скоростей;
- Коррекция поля давления с учётом обновлённого поля скорости;
- Обмен информацией с DEM расчётом (поле скорости, поле давления).
Результаты и выводы
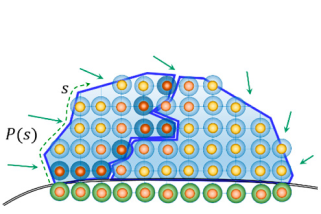
В работе было проведено моделирование обтекания цилиндра потоком воздуха в трубе прямоугольного поперечного сечения. Было рассчитано 8 секунд процесса, по результатам расчёта были сделаны следующие выводы: метод дискретных элементов хорошо подходит для моделирования адгезии ледяных кристаллов на поверхности модельного тела, максимальная толщина ледяного нароста по нормали к обтекаемому телу составила 2 см, средняя толщина ледяного нароста по нормали к обтекаемому телу составила 1 см, угол налипания снежной корки составил 110 градусов (Рис. 3).
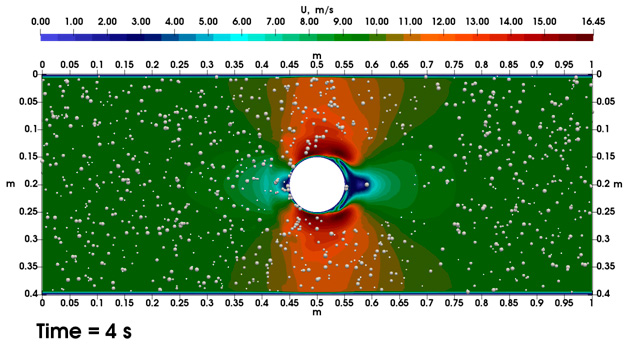
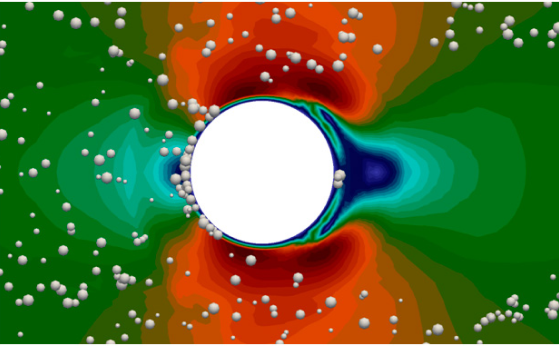
Данный подход представляется перспективным в силу возможности моделировать напряжённо-деформированное состояние ледяной корки, процесс её разрушения, взаимодействие частиц сложной формы.
Перечень публикаций за 2020 г.
-
Кошелев К.Б., Мельникова В.Г., Стрижак С.В. Разработка решателя iceFoam для моделирования процесса обледенения.
-
Мельникова В.Г., Кошелев К.Б., Стрижак С.В.
Моделирование обтекания профиля газокапельным потоком и расчет толщины жидкой пленки. Тезисы докладов, представленные на XXIV Международную конференцию «Нелинейные задачи теории гидродинамической устойчивости и турбулентность». 2020. с. 67.
-
K.B. Koshelev, V.G. Melnikova, S.V. Strijhak.
USING A THERMODYNAMIC FILM MODEL BASED ON SHALLOW WATER THEORY AND A DYNAMIC MESH MODEL FOR THE ICING OF 2D/3D BODIES IN THE ICEFOAM SOLVER SIMULATION. // Int. Conf. on the Methods of Aerophys. Research (Novosibirsk, Russia, November 1-7, 2020): Abstracts. Pt. I. Novosibirsk: Parallel, 2020. P. 123-124.
Перечень конференций за 2020 г.
-
С.В. Стрижак, К.Б. Кошелев, В.Г. Мельникова.
Разработка решателя iceFoam для моделирования процесса обледенения. Международная конференция «Иванниковские чтения». Орел, 25-26.09.2020.
-
Д.И. Романова, С.В. Стрижак.
Моделирование процесса обледенения цилиндра с помощью CFD-DEM подхода, используя пакеты YADE и OpenFOAM. Международная конференция «Иванниковские чтения». Орел, 25-26.09.2020.
-
Д.И. Романова, С.В. Стрижак.
МОДЕЛИРОВАНИЕ ПРОЦЕССА ОБЛЕДЕНЕНИЯ ДЛЯ МОДЕЛЬНОГО ТЕЛА C УЧЕТОМ ДВИЖЕНИЯ СНЕЖНЫХ КРИСТАЛЛОВ. Всероссийская конференция молодых ученых-механиков (YSM-2020) Сочи, «Буревестник» МГУ, 3-13 сентября 2020.
-
К.Б. Кошелев, С.В. Стрижак.
МОДЕЛЬ ПЛЕНКИ НА ОСНОВЕ ТЕОРИИ МЕЛКОЙ ВОДЫ ДЛЯ МОДЕЛИРОВАНИЯ ОБЛЕДЕНЕНИЯ ПРОФИЛЯ КРЫЛА И ЦИЛИНДРА. XXXI научно-техническая конференция по аэродинамике. Парк — отель «Яхонты». 29-30 октября 2020.
Результаты 2021 года работы
Прототип решателя iceFoam для моделирования обледенения на базе открытого пакета OpenFOAM v1912, получил развитие в виде библиотеки ICELIB, которая содержит три новых версии решателя: iceFoam1, iceDyMFoam2, iceDyMFoam3. В их основе – Эйлеров подход для газовой фазы, Лагранжев подход для моделирования движения капелек воды, а также модель мелкой воды для описания пленки жидкости на поверхности профиля. Каждая из версий предназначена для определенного типа задач.
iceFoam1 предназначен для оценки области обледенения 3D крыла, при условии, что толщина слоя льда достаточно мала и изменением поверхности профиля при обледенении можно пренебречь. Две другие версии направлены на моделирования обледенения рыхлым (rime) и гладким (glaze) льдом и учитывают влияние изменения геометрии профиля. Решатель iceDyMFoam2 лучше моделирует различные типы льда, однако ограничен количеством вычислительных ядер для параллельных вычислений, в отличие от iceDyMFoam3.
Для верификации решателей проведена серия расчетов обледенения различных 2D профилей (NACA 0012, GLC-305, General Aviation, Business Jet, Commercial Transport) и 3D стреловидного крыла. Отклонение результатов расчета от экспериментальных данных не превышало 10%.
Расчет 3D стреловидного крыла с профилем GLC-305 проводился в области, ограниченной параллелепипедом размера 7 м × 3 м × 3 м. Расчетная адаптивная неструктурированная сетка содержала порядка 1.3 × 106 узлов и включала в себя две области: пристеночную подобласть пленки с высотой в одну расчетную ячейку (характерный размер ячейки порядка 4 мм) и внешнюю подобласть для моделирования газокапельного потока. На рис. 1 изображена сетка с 5 уровнями адаптации. Расчеты проводились для режима «rime ice»: скорость несущего потока V=90 м/c, угол атаки 6° температура воздуха T = 261.87 K, водность LWC=0.51 г/м3, диаметр частиц d=14.5 мкм, время обледенения t=300 с. Расчетный шаг 6 × 10-5 с. Расчет осуществлялся версией iceDyMFoam3 на вычислительном кластере HPC4 НИЦ «Курчатовский Институт» (http://ckp.nrcki.ru/) 33 часа на 24 вычислительных ядрах.

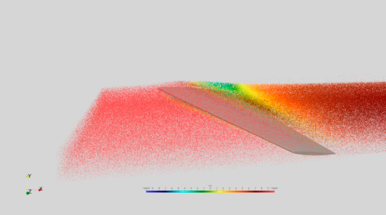

На рис. 2 показана вертикальная составляющая скорости капель воды с видом сверху. По максимальной толщине льда (примерно 3 мм) и по форме результаты моделирования близки к данным эксперимента, что говорит о возможности решателя моделировать существенно трехмерные процессы обледенения.
Другое направление – развитие моделей динамики и дробления переохлажденных капель при ударе о поверхность. В рамках Лагранжева подхода капли представлены сферическими частицами, на которые действуют силы аэродинамического сопротивления и тяжести. Для моделирования динамики рассматривались капли в форме сфероида, вследствие чего к рассмотрению добавлялись подъёмная сила, а также вращательный момент силы. Реализован программный комплекс для расчета плоских траекторий частиц сфероидной формы во внешнем аэродинамическом поле.
Проведено численное моделирование движения переохлажденных капель воды вблизи цилиндра при скорости смешанного потока 9 м/с, температуре 268К и интенсивности турбулентных пульсаций на левой границе 5 %. Расчет аэродинамических полей вблизи цилиндра осуществлялся с использованием модели турбулентности k-omega SST. Вязкость воздуха определялась по формуле Сазерленда. Результаты моделирования показывают, что несферичность частиц приводит к дополнительному рассеянию, а максимальное значение коэффициента столкновения наблюдается для сферических частиц, что хорошо согласуются с другими моделями.
Рассмотрен и реализован алгоритм влияния турбулентных пульсаций несущего потока на траектории частиц с помощью уравнения Ланжевена в рамках предположения об их изотропности. Путем численного моделирования установлено, что турбулентные пульсации не оказывают существенного влияния на интегральный коэффициент захвата частиц. Получен критерий для оценки наличия дробления капель, соударяющихся с поверхностью, при обтекании тела для заданных параметров потока.
Проведен ряд численных экспериментов моделирования обтекания цилиндра смешанным потоком с параметрами: радиус капель от 5 до 100 мкм; радиус цилиндра 0.1 м, скорость набегающего потока 100 м/c, давление атмосферное; температура -10 oC. Установлено влияние дробления капель на интегральную разницу в распределении массовой и счетной концентраций капель. На рис. 3 изображены изменения размеров капель при их взаимодействии с цилиндром в газовом потоке. Влияние количества капель на распределение массовой концентрации незначительное.
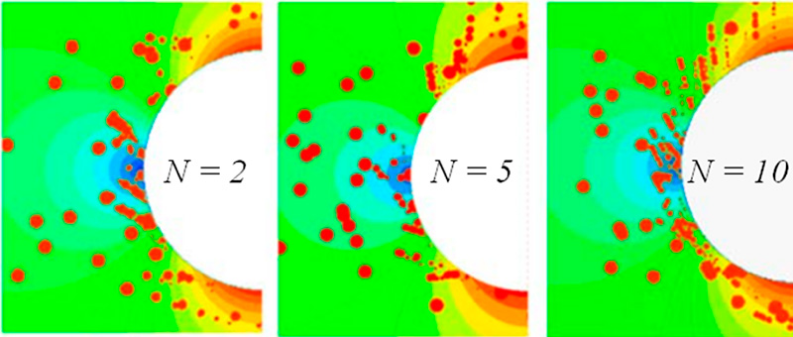
Представленные в работе результаты исследований могут быть использованы в расчетах обледенения и послужить основой в задачах противодействия этому явлению. Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-29-13016.
Перечень публикаций за 2021 г.
-
Кошелев К.Б., Осипов А.В., Стрижак С.В.
Особенности реализации решателя icefoam для решения задачи моделирования обледенения стреловидного крыла сверхзвукового самолета. В сборнике: Материалы XXII Международной конференции по вычислительной механике и современным прикладным программным системам (ВМСППС’2021). Материалы конференции. Москва, 2021. С. 394-395.
-
Стрижак С.В.
Разработка эффективного алгоритма параллельных вычислений для моделирования процесса обледенения стреловидного крыла с использованием решателя iceFoam. В книге: Математическое моделирование. Тезисы II Международной конференции. Москва, 2021. С. 79-81.
-
Кошелев К.Б., Осипов А.В., Стрижак С.В.
-
Амелюшкин И.А., Кудров М.А., Морозов А.О., Щеглов А.С.
Математические модели и методы расчета процессов, сопровождающих обледенение летательного аппарата. Труды Института системного программирования РАН. 2021. Т. 33. № 5. С. 237-248.
Перечень конференций за 2021 г.
-
С.В. Стрижак.
Разработка эффективного алгоритма параллельных вычислений для моделирования процесса обледенения стреловидного крыла с использованием решателя iceFoam. Устный доклад. С.В. Стрижак. Международная конференция «Математическое моделирование» г. Москва, МАИ, 21-22 июля 2021.
-
С.В. Стрижак, К.Б. Кошелев, А.В. Осипов.
Особенности реализации эффективного алгоритма параллельных вычислений для моделирования обледенения стреловидного крыла с профилем GLC-305. Устный доклад. Стрижак С.В. Международная конференция «Иванниковские чтения». г. Нижний Новгород, ИСП РАН, 24-25 сентября 2021.
-
К.Б. Кошелев, А.В. Осипов, С.В. Стрижак.
Особенности реализации решателя icefoam для решения задачи моделирования обледенения стреловидного крыла сверхзвукового самолета. Устный пленарный доклад. С.В. Стрижак. Двадцать вторая Международная конференция по Вычислительной механике и современным прикладным программным системам. г. Алушта, 4-13 сентября 2021.
-
И.А. Амелюшкин, М.А. Кудров.
Взаимодействие переохлажденных капель с рельефным телом в потоке газа. Стендовый доклад. М.А. Кудров. Двадцать вторая Международная конференция по Вычислительной механике и современным прикладным программным системам. г. Алушта, 4-13 сентября 2021.
-
В.Н. Корчагова.
Использование алгоритмов динамического перестраивания сетки при решении задач газовой динамики разрывным методом Галеркина. Устный доклад. В.Н. Корчагова. Всероссийский Аэроакустический Форум г. Геленджик, ЦАГИ, 20-25 сентября 2021.
-
К.Б. Кошелев, А.В. Осипов, С.В. Стрижак.
Применение решателя iceFoam для моделирования обледенения стреловидного крыла с профилем GLC-305. Устный онлайн доклад. С.В. Стрижак. XXVIII Всероссийская конференция с международным участием «Высокоэнергетические процессы в механике сплошной среды» г. Новосибирск, ИТПМ СО РАН, 20-24 сентября 2021.
-
Konstantin Koshelev, Andrey Osipov, Sergei Strijhak.
The simulation of a gas-droplet flow around a swept wing of a supersonic jet aircraft in order to determine ice accretion using iceFoam solver. Устный пленарный онлайн доклад на английском языке. С.В. Стрижак. Vth International Conference on Aerospace System Science and Engineering ICASSE 2021, 14-16 July 2021, Virtual Event.
Результаты проекта за 2022–2023 гг.
В настоящее время проектируются новые перспективные сверхзвуковые пассажирские самолеты. В связи с этим ведутся работы по проектированию и испытаниям самолета-демонстратора. Например, это модель самолета в рамках проекта НЦМУ «Сверхзвук» (Россия) и действующий проект самолета-демонстратора Lockheed Martin X-59 QueSST (США). Данный самолет-демонстратор совершает посадку и взлет на определенных высотах на дозвуковых скоростях. В процессе движения самолета-демонстратора в облаках существует вероятность возникновения процесса обледенения, которое является опасным явлением, так как снижает аэродинамические характеристики самолета. Образовавшийся лед бывает разных типов и формы: рыхлый, прозрачный, барьерный, смешанный, рогообразный, шероховатый. Поэтому необходимо проводить научные исследования по изучению данного явления. Одним из возможных подходов является моделирование нарастания льда с помощью численных моделей. В открытом доступе имеется 3D цифровая модель самолета-демонстратора X-59. В данном исследовании рассматривается только треугольное крыло сложной формы (Рис.1).
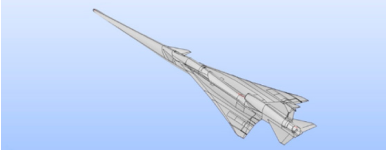

Обледенение крыла моделируется с помощью решателя iceFoam, разработанного в рамках пакета OpenFOAM. Для решения задачи используется две сетки: первая во внешней области, вторая — для жидкой пленки у твердого тела. Для построения сетки газовой фазы используются утилиты blockMesh и snappyHexMesh в составе пакета OpenFOAM. Расчеты были проведены для моделей крыла самолета-демонстратора X-59 в масштабе 1:25 и 1:1 для случая рыхлого льда. Для разномасштабных моделей обеспечивалось неизменность чисел Рейнольдса и Маха. В тоже время неизменными параметрами в размерном виде были водность воздуха и медианный диаметр капель воды. На рис.2 видна разница в положении областей обледенения на нижней поверхности фрагмента крыла для разномасштабных моделей.


Предварительный вывод — даже совпадения чисел Рейнольдса и Маха для несущей фазы недостаточно для разномасштабных моделей обледенения. Необходимо проводить дополнительные исследования c разными масштабами крыла.
Задача изучения процесса обледенения также актуальна в связи с эксплуатацией крупных кораблей и рыболовецких судов в морях Северного Ледовитого океана. В данном исследовании моделирование обледенения рыболовного судна выполнено при различных числах Рейнольдса и Фруда. С помощью решателя interDyMFoam определялось положение волн и брызг воды в пространстве при движении корабля с учетом волнения на море. С помощью решателя iceFoam моделировался процесс обледенения поверхности судна. Выполнены расчеты для среднего объемного диаметра капель 1000 микрон, скорости ветра 10 м/с и скорости корабля 5 м/с. На рис.3 приведены расчетные данные о положении пленки воды и намерзшего льда через 8 с.


Сформулирован оригинальный критерий режима дробления соударяющихся с поверхностью капель, зависящий от параметров аэрозольного потока для оценки наличия дробления при обтекании тела при заданных параметрах. Показано влияние дробления капель на интегральную разницу в распределении массовой и счетной концентраций капель. Представленные в работе результаты аналитических и численных исследований могут быть использованы в расчетах обледенения и послужить основой в задачах противодействия этому явлению. Впервые показано, что при обтекании тела газокапельным потоком зависимость увеличения за счет дробления массовой концентрации капель от начального размера капель (или соответствующего ему числа Вебера) немонотонна.
Определены зависимости концентрации, скорости и распределения частиц по размерам в пограничном слое воздушного потока у заснеженной поверхности в зависимости от основных управляющих параметров. Разработан численный алгоритм, проведены верификация и валидация результатов на основании имеющихся экспериментальных данных. Развиты модели динамики частиц в пограничном слое у поверхности обтекаемого тела.
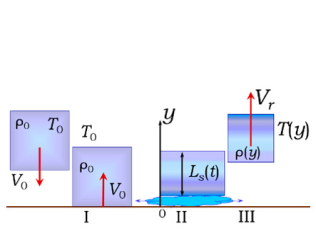
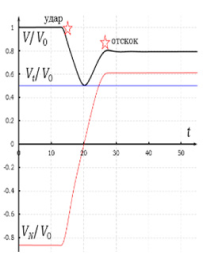
Развита физико-математическая модель и оригинальный метод расчета режимов взаимодействия кристаллов льда с нагретой поверхностью обтекаемого тела. Узлы расчетной сетки деформируются при изменении нагрузок в течение времени удара кристалла о поверхность нагретого тела, между ячейками рассчитываются тепловые потоки и передача импульсов, при плавлении ячейки удаляются в течение времени на основании скорости уноса массы в процессе удара кристалла о поверхность обтекаемого тела. Метод также применен для расчета возникновения напряжений и разрушения льда на крыле под действием аэродинамических и механических нагрузок. Разработанный метод и численный алгоритм его реализации могут быть использованы при расчете обледенения для случаев длительного времени нароста наледи и для расчета параметров вибрационных и деформационных противообледенительных систем. В настоящем исследовании он был впервые применен к задаче определения параметров теплообмена кристалла при его столкновении с твердым телом с учетом вязкости твердого тела и перехода кинетической энергии движения слоев твердого тела и их деформации в тепловую энергию за счет вязкости твердого тела.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-29-13016.
Перечень публикаций за 2022–2023 гг.
-
Стрижак, С.В.
Развитие модели нейронной сети iceMPLNet для предсказания формы льда / С.В. Стрижак, К.Б. Кошелев, Д.И. Романова // Материалы XIV Международной конференции по прикладной математике и механике в аэрокосмической отрасли (AMMAI’2022) : Материалы конференции, Алушта, 04–13 сентября 2022 года. – Москва: Московский авиационный институт (национальный исследовательский университет), 2022. – С. 396-399.
-
Стрижак С.В.
Алгоритм исключения «плохих» расчетных ячеек для моделирования процесса обледенения крыла самолета / С.В. Стрижак, К.Б. Кошелев, А. В. Осипов // Авиация и космонавтика: тезисы 21-ой международной конференции, Москва, 21–25 ноября 2022 года / Московскийавиационный институт (национальный исследовательский университет). – Москва: Издательство «Перо», 2022. – С. 425-427.
-
Koshelev, K.B.
Investigation of ice growth on a swept wing with considering the model of uniform roughness / K.B. Koshelev, A.V. Ivanov, S.V. Strijhak // ХХI International Conference on the Methods of Aerophysical Research (ICMAR 2022): Abstracts, Novosibirsk, 08–14августа 2022 года. Vol. Part I. – Novosibirsk: Федеральное государственное бюджетное учреждение «Сибирское отделение Российской академии наук», 2022. – P. 102-103. – DOI 10.53954/9785604788967_102.
-
Кошелев, К.Б.
Особенности построения сетки для моделирования процесса обледенения треугольного крыла сложной формы / К.Б. Кошелев, А.В. Осипов, С.В. Стрижак // Труды Института системного программирования РАН. – 2022. – Т. 34, № 5. – С. 215-226. – DOI 10.15514/ISPRAS-2022-34(5)-15.
-
Konstantin Koshelev, Andrey Osipov, Sergei Strijhak, Nikita Tryaskin.
-
K. Koshelev, A. Osipov. S. Strijhak.
Using the iceFoam solver to simulate ice accretion process on a swept wing with GLC-305 airfoil. February 2023, AIP Conference Proceedings 2504(1):030028 , DOI: 10.1063/5.0132710
-
Амелюшкин И.А.
Математические модели, численные алгоритмы, результаты исследования особенностей обледенения летательных аппаратов // XXVI Всероссийский семинар с международным участием по струйным, отрывным и нестационарным течениям: материалы докладов. Санкт-Петербург, 27 июня – 1 июля 2022 года / Сост.: М.В. Чернышов, А.С.Капралова. – СПб.: Балт. Гос. Техн. Ун-т, 2022. С. 26–27.
-
Amelyushkin I.A.
Models of interaction of snow particles and supercooled droplets with a solid body in nonhomogeneous flow, DOI: 10.53954/9785604788974_11 // Abstracts from International conference on the methods of aerophysical research, August 8–14, 2022 Novosibirsk, Russia, Part II, P. 11–12.
-
Амелюшкин И.А., Кудров М.А., Морозов А.О.
Модели сальтации снега, динамики кристаллов и переохлажденных капель в газовых потоках // Всероссийская конференция молодых ученых-механиков YSM-2022. Тезисы докладов (4 − 14 сентября 2022 г., Сочи, «Буревестник» МГУ). – М.: Издательство Московского университета, 2022. – C. 37. – (Электронное издание сетевого распространения), ISBN 978-5-19-011787-5 (e-book).
-
Амелюшкин И.А.
Особенности динамики частиц снега, льда и переохлажденных капель в пограничном слое у нагретой поверхности и в цилиндрическом канале // Модели и методы аэродинамики. Материалы Двадцать второй международной школы-семинар. – М.: ЦАГИ, 2022.
-
Амелюшкин И.А., Кудров М.А., Морозов А.О.
Модели процессов, сопровождающих обледенение летательных аппаратов и развитие противообледеннительных систем // Материалы ХХXIII научно-технической конференции по аэродинамике в пос. им. Володарского. – М.: Изд-во ЦАГИ. – 2022. С. 18–19.
-
Амелюшкин И.А., Кудров М.А., Морозов А.О.
Деформация, разрушение и плавление льда при соударении с нагретой поверхностью и при аэродинамическом воздействии // Труды 65-й Всероссийской научной конференции МФТИ» – 6–7 апреля 2023. МФТИ.
-
Амелюшкин И. А.
Особенности обтекания тела потоком, содержащим переохлажденные капли. Вестник МГОУ. 2022. 6-15 с. DOI: 10.18384/2310-7251-2022-1-6-15.
Участие в конференциях за 2022–2023 гг.
-
Международная конференция по Прикладной математике и механике в аэрокосмической отрасли (AMMAI’2022), 4-13 сентября 2022 г., г. Алушта. Стрижак С.В. Устный доклад.
-
International conference on the methods of Aerophysical Research, August 8–14, 2022 Novosibirsk, Russia. Кошелев К.Б. Устный доклад.
-
International conference on the methods of Aerophysical Research, August 8–14, 2022 Novosibirsk, Russia. Амелюшкин И.А. Устный доклад.
-
4. 21-я Международная конференция «АВИАЦИЯ И КОСМОНАВТИКА», 23.11.2022 г. Москва. Стрижак С.В. Устный доклад.
-
XXVI Всероссийский семинар с международным участием по струйным, отрывным и нестационарным течениям: материалы докладов. Санкт-Петербург, 27 июня – 1 июля 2022 года. Амелюшкин И.А. Устный доклад.
-
Всероссийская конференция молодых ученых-механиков YSM-2022. Тезисы докладов (4 − 14 сентября 2022 г., Сочи, «Буревестник» МГУ). Амелюшкин И.А. Устный доклад.
-
Модели и методы аэродинамики. Материалы Двадцать второй международной школы-семинар. – М.: ЦАГИ, 2022. Амелюшкин И.А. Устный доклад.
-
ISP RAS OPEN 2022, Москва. Кошелев К.Б. Устный доклад.
-
The 6th Symposium on Computational Marine Hydrodynamics. 第六届CMHL船舶与海洋工程计算水动力学研讨会 (The 6th CMHL Symposium 2023). Shanghai, China. January 14, 2023, Online Virtual Meeting. Стрижак С.В. Пленарный доклад.
-
65 Всероссийская научная конференция МФТИ» – 6–7 апреля 2023. МФТИ. Амелюшкин И.А., Кудров М.А. Устный доклад.